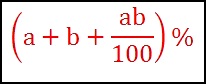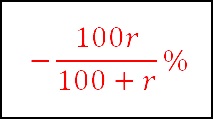Dealing with Percentages – Part 2

• Percentage as Fractions
• Percentage Change
• Changing Quantities by Percent

I would like to discuss a few more ideas in this post. Let us begin.

Successive Percentage Change:

I am sure that you would have seen retail stores with offers like “50% + 40% off”. If my memory serves me right, these types of offers were made extremely popular by Koutons. I always thought of it as a “90% off” offer but clearly I was wrong. I guess some of you might have made the same mistake as well. A “50% + 40% off” does not mean a “90% off”. It actually means that you will be given a discount of 50% first and then on the reduced price you will be given another 40% discount.

Let us calculate to figure out how much this actually means.

Let us assume that the T-shirt you are trying to buy costs Rs. 100. A 50% discount would bring down the price of the T-shirt to Rs. 50. Another 40% discount on the reduced price of Rs. 50 would further bring down the price by Rs. 20 (which is 40% of 50), to Rs. 30. So, the price has effectively gone down from Rs. 100 to Rs. 30 which means that the effective discount has been 70% and not 90%.

Let me ask you another question. Try to answer it in your head before you actually scroll down and check the answer.

(Join the InsideIIM Test Prep group on Facebook here)

Example 1: 

Shop A is selling a T-shirt at a discount of 50% + 40% on the MRP whereas shop B is selling the same T-shirt at a discount of 40% + 50%. Should you buy the T-shirt from Shop A or Shop B?

Now, there may be a few things going on in your head like ‘A’ is better because it is offering the higher percentage first or ‘B’ is better because it is offering the higher percentage later or this cannot be determined until and unless we know the MRP of the T-shirt. Well, stop your internal monologue! The answer is that it would not make a difference whether you buy it from Shop A or from Shop B. Don’t believe me? Do the math!

Let us assume that the MRP of the T-shirt is ‘x’

From Shop A, a 50% discount would bring down the price to 0.5x and another 40% discount would bring down the price to 0.3x

From Shop B, a 40% discount would bring down the price to 0.6x and another 50% discount would bring down the price to 0.3x

As you can see, the sale price is the same in both cases.

In case you are wondering as to why it is the same in both cases, it is because percentages are multiplicative in nature and p*q is always the same as q*p.

For future reference, you can use this formula for effective % change in case of successive % changes of a% and b%:

Note: Please keep in mind the ‘+’ & ‘-’ signs while using this formula.

If you put a = 50% and b = 40% (from the above example), you would get 110%, which would be the incorrect answer. You should use -50% and -40% to get the correct answer of -70%. You will have to use negative values for the above example because the % changes considered are discounts.

Example 2:

A company’s revenue grew by 10% and 20% in 2009 and 2010 but fell by 25% in 2011. What was the net % change?

Use the formula for the first two years = 10 + 20 + 10*20/100 = 32

Combine this with the last year = 32 – 25 + (32)(-25)/100 = 7 – 8 = -1%

Compensating Percentage Change:

I am sure that you must have encountered questions like these:

a)     The price of beer has gone up by 25%. By how much should you reduce your consumption so that your expenses do not change?

b)     Ravi got a salary hike of 10%. The new boss thought this shouldn’t have happened because Ravi doesn’t deserve it, so he slashes Ravi’s salary by 10%. Is Ravi back to the original? If no, then by what % should Ravi’s boss reduce his salary?

Now there are a couple of ways of doing these questions. One is by using the concepts of fractions, proportionality, etc. The other one is by using the formula. Let us discuss both of them.

a)     Price of beer has gone up by 25%

•  Price of beer has increased by 1/4^th
•  Price of beer has become 5/4^th
•  Consumption should become 4/5^th
•  Consumption should be reduced by 1/5^th
•  Consumption should be reduced by 20%

b)     A hike of 10% and then a reduction of 10% won’t be fair as Ravi would end up getting less than the original. Using the successive % change formula {10 – 10 + 10*(-10)/100 = -1}, we can say that he would end up getting 1% lesser than the original. To get the correct deduction value:

Ravi’s salary was hiked by 10%

• Ravi’s salary has increased by 1/10^th
• Ravi’s salary has become 11/10^th
• To go back to the original, it should become 10/11^th of the current value
• It should be reduced by 1/11
• It should be reduced by 9.09%